Über das Material
Insgesamt gibt es für die Primarstufe Diagnose- und Fördermaterialien zu den Inhaltsbereichen:
- Natürliche Zahlen (ab Klasse 3)
Leitideen
Das Mathe sicher können Material verfolgt den Grundgedanken der diagnosegeleiteten Förderung und hat als Ziel schwächere Schülerinnen und Schüler gezielt zu identifizieren und sie entsprechend zu fördern. Alle Materialien basieren auf den drei folgenden Leitideen:
Diagnosegeleitetheit
Kenntnisse und Vorstellungen der Lernenden werden mittels Standortbestimmungen erhoben, um diese daran anschließend gezielt zu fördern
Verstehensorientierung
Nachhaltiges und sinnstiftendes Lernen orientiert sich am Aufbau von Verständnis; dazu gehört der Rückbezug auf motivierende außermathematische Kontexte und vor allem auf strukturelle, innermathematische Vorstellungen und Darstellungen.
Kommunikationsförderung
Der Aufbau von Verständnis bedarf gerade bei schwächeren Lernenden der Kommunikation untereinander und mit der Lehrperson.
Die Materialien wurden auf wissenschaftlicher Basis und in enger Zusammenarbeit mit zahlreichen Projektschulen erprobt und weiterentwickelt.
Aufbau
Jeder Inhaltsbereich besteht aus mehreren Förderbausteinen. Diese Bausteine sind in zentrale Basiskompetenzen aufgeteilt, die alle Schülerinnen und Schüler haben sollten. Mit Hilfe der im Projekt entstandenen Materialien können diese Basiskompetenzen durch themenspezifischen Diagnoseaufgaben („Standortbestimmungen“) mit der gesamten Klasse erhoben werden.
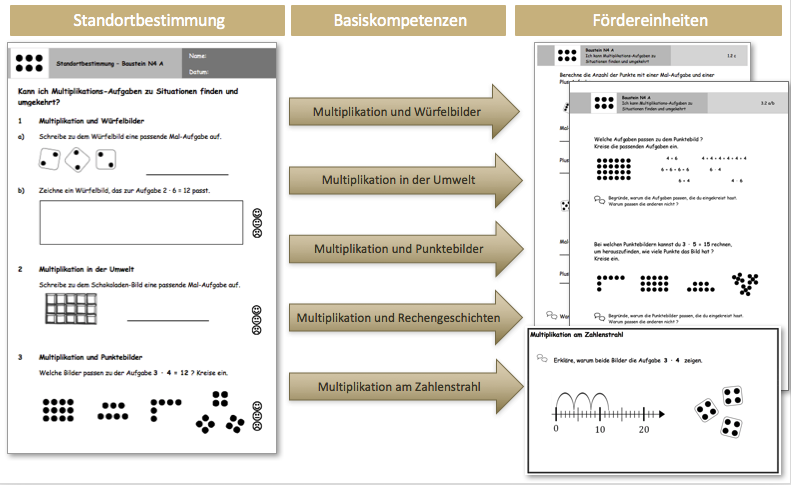
Standortbestimmungen und Fördereinheiten
Die Standortbestimmungen können mit einer gesamten Klasse durchgeführt werden, um Kinder mit Schwierigkeiten in dem jeweiligen Bereich zu identifizieren und für eine Förderung auszuwählen. Sie sind in Basiskompetenzen unterteilt, die sich an den Verstehensgrundlagen orientieren. Anhand der Bearbeitung der Standortbestimmung durch die Kinder erhält die Lehrkraft einen Eindruck über ihre bereits vorhandenen Fähigkeiten und die individuellen Schwierigkeiten. Sie geben der Lehrkraft Aufschluss darüber, welche Fördereinheiten mit den Schülerinnen und Schülern durchzuführen sind, da zu jeder Diagnoseaufgabe eine passende Fördereinheit gehört. In dem didaktischen Kommentar werden Hinweise zur Auswertung der Standortbestimmungen gegeben.
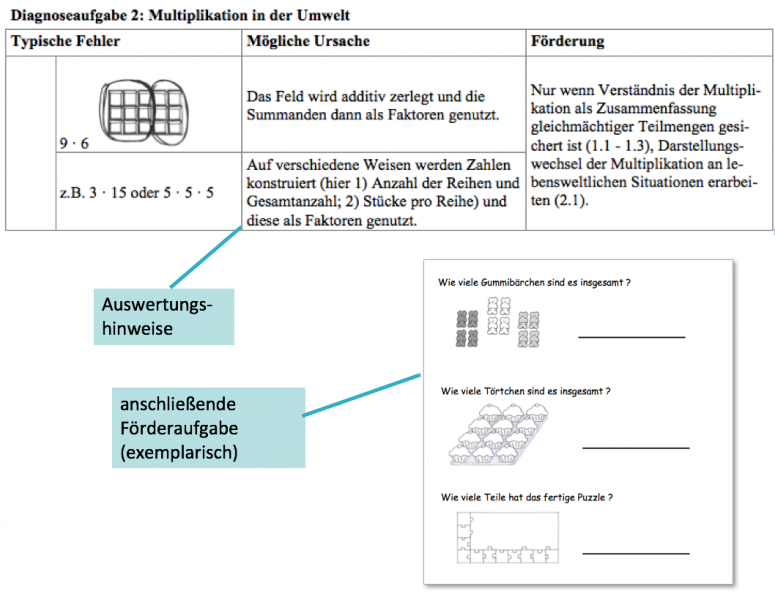
Auswertungshilfen
Auswertungshilfen helfen, die Standortbestimmungen schnell auszuwerten und den individuellen Förderbedarf der Lernenden zu bestimmen. Neben einer angebotenen Musterlösung wird auch auf typische Fehler, deren mögliche Ursachen eine entsprechende Förderung verwiesen.
Die Lehrkraft erhält auf diese Weise Informationen über bereits vorhandenen Fähigkeiten und Schwierigkeiten der Lernenden. Zu jeder Diagnoseaufgabe gehört eine passende Fördereinheit. So kann individuell entschieden werden, welche Basiskompetenzen in der Kleingruppe erarbeitet und gefestigt werden.
Didaktischer Kommentar
Neben den Hinweisen zur Durchführung und Auswertung der Standortbestimmungen enthält der didaktische Kommentar vor allem Hinweise zu den Diagnose- und Förderbausteinen. Das didaktische Hintergrundwissen gliedert sich dabei stets in die Bereiche:
- Lerninhalt
- Veranschaulichung und Material
- Aufbau der Förderung
- Weiterführende Literatur
Diagnose und Fördermaterialien für die Primarstufe
Zum Inhaltsbereich Natürliche Zahlen gibt es insgesamt 15 Förderbausteine. Je Baustein umfasst das Material für die Primarstufe:
- Handreichungen mit didaktischen Hintergrundinformationen zu dem jeweiligen Baustein zur Vorbereitung und Begleitung des Einsatzes der Materialien
- Diagnose- und Fördermateial Primar gesamt, welches die Standortbestimmung sowie das komplette Fördermaterial umfasst
- Materialordner mit verschiedene Einzeldateien aus dem Gesamtmaterial, um eine gezielte Auswahl von Materialien zu erleichtern:
- Standortbestimmung
- Übersicht über das Diagnose- und Fördermaterial des Bausteins
- Fördermaterial für Schülerinnen und Schüler
- Impulskarten und Aufgabengeneratoren
- Sprachbildungsmaterial
- Zusatzmaterial
